Models and Methods
Principle of GBHM
GBHM (Geomorphology-Based Hydrological Model) is a distributed hydrological model which is based on the catchment geomorphological properties.
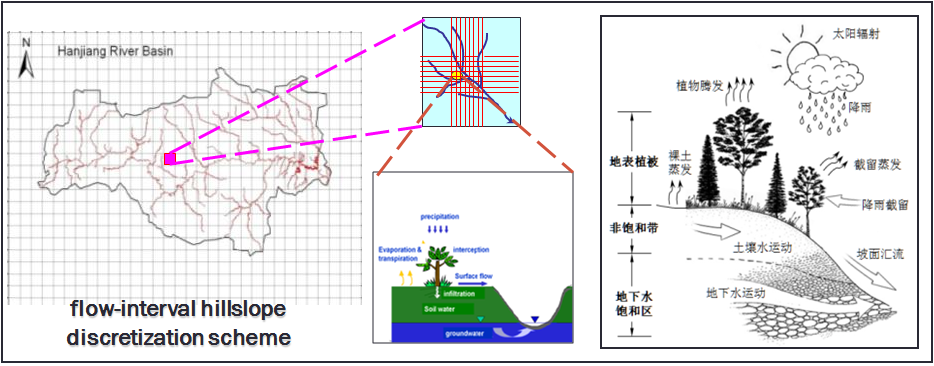
Simulation of the hydrological processes in GBHM included two main components: hydrological simulation at each hillslope and river routing in the river network. The figure above describes the flow-internal hillslope discretization scheme. While the river network was generated using a flow accumulation method, the whole watershed was divided into many sub-catchments linked by the river network and coded using the Pfafstetter coding system. Each sub-catchment was divided into several flow intervals according to the flow distance from each grid to the catchment outlet, so that all of the grids in the same flow interval were of equal flow distance. Hydrological simulation was carried out in each grid, and the runoff in the grids were added together to obtain the total runoff in each flow interval. Details of the model can be found in references [1][2].
Extended Streamflow Prediction
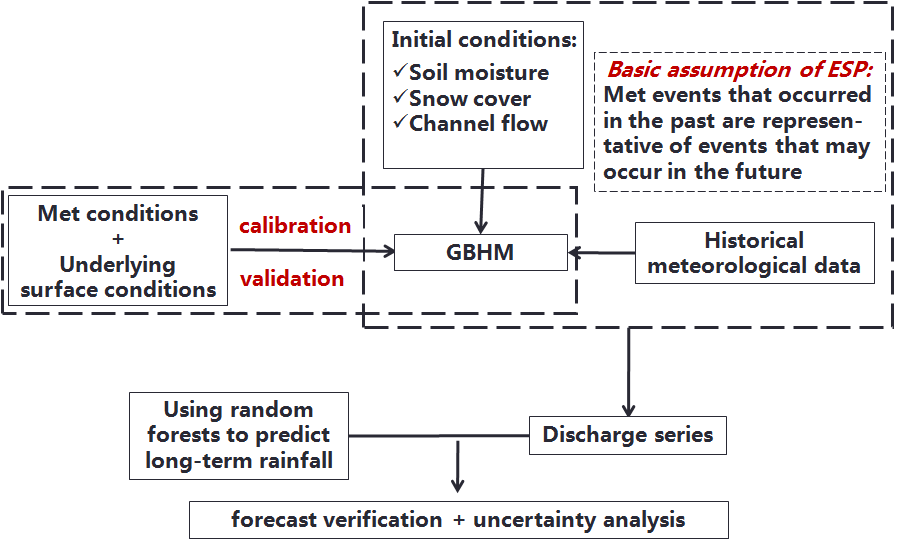
This section will explain the main method conducted in this study, Ensemble Streamflow Prediction (ESP). Procedures can be illustrated in the figure below. Using meteorological conditions and underlying surface conditions, we can calibrate and validate GBHM. This is the first thing we need to do in order to use ESP method. The basic assumption of ESP is meteorological events that occured in the past are representative of events that may occur in the future. Based on this, we use GBHM to get the initial conditions, like soil moisture, snow cover, channel flow and so on. Given the current initial conditions, we use historical time series of precipitation and temperature as the required ensemble forcing. Then we can get the discharge series and usually the mean value of the series will be regarded as the forecast request. The above regular steps are for conventional ESP. However, the problem is that the member of the discharge series has the same weight and this may not be appropriate. For example, if the forecast year has much more rain, then we need to select the wetter meteorological series as the forcing input, dry years' meteorological conditions will affect the forecast. This study use Random Forecasts to predict the long-term rainfall in order to select the future possible precipitation scenarios from the historical meteorological records based on the similarity of the selected climatic factors.
Random Forests
Random Forecasts is the improved decision tree model which is based on Bagging (bootstrapping + aggregating) method. The bagging method can make up the overfitting problem confined by machine learning models. As shown in the figure below, the basic idea of bagging is that: although the result of each individual model is subject to overfitting induced by stochastic errors in the training samples, the aggregated results of multiple models may not subject to overfitting as the effect of multiple stochastic error scanarios tend to be offset by each other. In bagging, multiple stochastic error scenarios are realized through independently and randomly selecting training sets from the total historical observation set; aggregating of forecast of each individual trained model is realized by taking their arithmetic mean value. In Random Forests model, the decision tree model is selected as the individual forecast model.

Besides forecast, Random Forests can also evaluate the importance of explanatory variables to the explained variable, following a simple rule "the more relevant the explanatory variable, the larger effect it exerts on the forecast" so that we can use Random Forests model for variables selection. In bootstrap sampling, for each individual model, the total observations are splitted into two groups: in-bag subset (i.e., training subset) and out-of-bag subset; the out-of-bag subsets can be used to evaluate the importance of each explanatory: 1) randomizing the values corresponding to one selected explanatory variable in out-of-bag subests; 2) using the randomized out-of-bag subset and the original model to make new forecast; 3) measuring the importance of the selected explanatory variable by the increase in mean square error of the new forecast. My study employs the R-cran Random Forests package for climatic index importance evaluation.