The content of an article below could be different what originally
published in the above journal. Some figures have been updated
using the latest data.
The estimated vapor flux convergence is compared with the observed discharge data in the Chao Phraya river basin, Thailand. The mean annual values are not identical, but their seasonal change corresponds very well.
The four year mean vapor flux convergece is also compared with the climatolological runoff of nearly 70 large rivers. The multi-annual mean runoff is calculated from the GRDC (Global Runoff Data Centre) data set and used for the comparison. There is generally good correspondence between atmospheric water balance estimates and the runoff observations on the ground, especially in the mid and high latitudes of northern hemisphere. However, there are significant differences in many cases. The results emphasize the importance of accurate routine observations of both the atmosphere and river runoff.
The global water balance of the zonal mean is compared to prior estimates, and the estimated value from this study is found to be smaller than previous estimates. Annual water balance in each ocean and each continent are also compared with previous estimates. Generally, the global runoff estimation using conventional hydrological water balance is larger than the result by the atmospheric water balance method.
Annual fresh water transport is estimated by atmospheric water balance combined with geographical information. The results show that the same order of fresh water is supplied to the ocean from both the atmosphere and the surrounding continents through rivers. The rivers also carry approximately 10% of the global annual fresh water transport in meridional directions as zonal means.
Keywords : atmospheric water balance method, continental hydrology, large scale evapotranspiration, total water storage in river basin, fresh water transport
Water balance is the most fundamental aspect of the hydrological cycle. Traditionally, water balance has been estimated using observational data at ground surface. Currently, there are many studies in progress that seek to observe or to estimate evapotranspiration and precipitation over large spatial scales using radar or satellite remote sensing. However, it is still difficult to obtain very reliable estimates. On the other hand, water balance estimation using atmospheric data, namely the atmospheric water balance method, is becoming easier to apply than before due to the availability of high resolution atmospheric data.
Three important research areas that need to be investigated by hydrologists addressing the problems of global change are:
This study made an attempt to estimate the water balance in both river basins and over the global domain using the atmospheric water balance method. The basic concepts of the atmospheric water balance method are presented in section 2. The atmospheric data and data handling algorithm are described in section 3. In section 4, the atmospheric water balance method was applied to the Chao Phraya river basin, in Thailand. A part of this section was presented in IUGG/IAHS 1991, Vienna [Oki et al.1991]. The estimated atmospheric water balance is validated by river discharge data and by prior estimates, in section 5. Annual freshwater transport from the continents to the oceans and the meridional means are also estimated. A part of this section was presented in IAMAP/IAHS 1993, Yokohama [Oki et al.1993].
It is well known in the field of climatology that vapor flux convergence gives water balance information that can complement the traditional hydrological elements such as precipitation, evapotranspiration and discharge [Peixoto and Oort1983]. The basic concept of using atmospheric data to estimate terrestrial water balance was firstly presented by Starr and Peixoto [1958]. The application of this concept to regional studies [Rasmusson1968] or the region and period with special observations Peixoto[1970], has been troublesome because there were only a few scattered observation stations of upper air soundings Bryan and Oort[1984]. Quite recently, Brubaker et. al interpolated these upper air sounding data onto a regular grid and analyzed the atmospheric water vapor fluxes over the Northern and Southern American Continents. Rasmusson[1977] suggested that such a method to estimate regional water balance using vapor flux convergence should be very useful and accurate for climatological estimates over areas larger than 10^6 km^2 and over monthly or longer periods, with the operational rawin sonde network and current observational schedules. Previously, ``Objective Analyses Data'' have been prepared to the context of prescribing initial values for daily numerical weather forecasting, using GCM and various observational data [Daley1991]. Now, such data sets have indeed become available, and their spatial resolution seems much more improved than the operational rawinsonde network. Therefore it is worth to apply such latest atmospheric data for the estimation of the water balance in river basins.
The atmospheric water balance is described by the equation,
where,
,
,
,
,
, and
,
represent precipitable water (column storage of water vapor),
column storage of liquid and solid water,
vertically-integrated two-dimensional vapor flux,
vertically-integrated two-dimensional water flux in the liquid and solid
phases, evapotranspiration, and precipitation, respectively.
These terms are shown in Fig. 1(a).
The term 
represents the horizontal divergence.
is the vapor flux vector,
and the components are directed towards east and north;
,
,
,
,
, and
represent specific humidity, wind velocity E-W and N-S,
gravitational acceleration,
pressure at the point and pressure at ground surface.
Water vapor flux convergence is computed
assuming that the earth is a sphere which has radius of
.
Generally, the water content in the atmosphere in the solid and liquid phases is negligible, and equation (1) is simplified as:
The water balance of river basin is described as,
where 
represents
the storage in the basin, and
and
represent surface runoff and the ground water movement, respectively.
includes snow accumulation
in addition to soil moisture and ground water storage.
If the area of water balance is set within an arbitrary boundary,
represents the net outflow
from the region of consideration
(i.e. the outflow minus inflow from surrounding areas).
In this study, all ground water movement is considered
to be observed at the gauging point of the river
(
),
and equation (7) becomes:
With respect to the term of 
,
equations (6)
and (8) are combined into:
The following further assumptions are employed in the annual water balance computations:
).
).
In this simplified equation, the water vapor convergence
(precipitation-evaporation) and runoff
are equal over the annual period.
If a river basin is selected as the water balance region,
is
simply the discharge from the basin.
The large-scale mean evapotranspiration can be estimated if large-scale mean precipitation is available. The equation
is obtained from equation (6) without annual mean assumptions which is then applicable over shorter periods. If atmospheric data and precipitation data are available over short time scales such as months or days, evapotranspiration can be estimated at the corresponding time scales. The region over which to estimate evapotranspiration is not limited to a river basin but depends only on the scale of atmospheric and precipitation data.
The atmospheric water balance method to estimate large scale evapotranspiration thus complements the traditional river basin water balance, which calculates annual evapotranspiration as a loss within a river basin.
From the equations (8) and (6), we obtain
which indicates the change of basin water storage
can be estimated
with atmospheric and runoff data. Even though an initial value is required
to obtain the absolute value of storage,
the atmospheric water balance can be useful in estimating the
seasonal change of total water storage in a river basin.
Accurate measurements can be carried out in comparatively small river basins in order to observe areal evapotranspiration. However, it is practically impossible to measure evapotranspiration over large continental scale catchments. In such a case, the atmospheric water balance method using atmospheric data and precipitation data (equation 11) will offer another way to obtain the areal evapotranspiration.
Total water storage in river basins is one of the very important state variables of hydrological processes, which is directly related to the discharge and surface soil moisture. Generally that is also very difficult to be measured except for a tiny experimental river basin with intensive observations. The atmospheric water balance method utilizing runoff data (equation 12) will provide this key information of hydrological processes in large river basins. Further investigation shall be made in the near future to analyze the relationship between storage and runoff, and storage and evapotranspiration.
Many papers in this special issue are concerned with methods for estimating
the macro-scale hydrological processes from observations and by models.
The atmospheric water balance method has the capability to provide
the macro-scale validation data for them.
In the case of intensive hydrological field observations,
it is desirable to design a rawinsonde observational network
which encloses the region of concern. Then, the atmospheric water balance
will estimate the areal mean evapotranspiration and the change of total
water storage in the area. The required time intervals of the atmospheric
observation depend on the spatial scale.
The relationship 
may be referred to determine
the intervals. Let wind velocity
be 10 m/s and horizontal distance 
be 100 km, it will be better to make observations
by intervals of 
3 hour or less.
On the contrary, twice daily
(i.e. 
12 hour) data
can provide a good estimation for the horizontal scales of approximately
400-500 km or more.
Another advantage of the atmospheric water balance method is the data availability. It is not easy to collect the discharge data and cover all the continents by observed runoff data. Even though the spatial density of observational network varies among regions, the atmospheric data covers the whole world and there are fewer political problems to be faced when handling this data. In this paper, equation 10 is basically used for the quantitative examination of both the atmospheric and discharge data. It can be also used to estimate the global distribution of discharge.
The meridional distribution of the zonally-averaged annual energy
transport by the atmosphere and the ocean is well known and has been
discussed [Masuda1988a].
However, a corresponding distribution of water transport
has not often been studied although the cycles of energy and water are
closely-related. Wijffels et. al[1992]
used the 
from
Bryan and Oort[1984] and discharge data from
Baumgartner and Reichel[1975] and estimated
the freshwater transport of the ocean and atmosphere, but not by the rivers.
The annual water transport in the north-south direction over
continents 
and oceans 
can be estimated
from the vertically integrated vapor flux convergence
with geographical information and river discharge.
The governing equations can be written as:
where 
represents the total discharge from continents to the oceans
at latitude 
,
and 
represents the longitude.
and
mean
the zonal integration only over land and sea respectively.
The European Centre for Medium Range Weather Forecasts (ECMWF) produces the ``Objective Analysis'' dataset, made through the ``4-dimensional data assimilation system'' [Hoskins1989], and used as initial values in weather forecasting. This method is based on dynamically-consistent temporal extrapolation using a GCM and statistical spatial interpolation of observed data using the ``optimum interpolation method'' [Daley1991]. Rawinsondes, satellite temperature and moisture, cloud track winds, surface observations by ships, ocean buoys, land stations, aircraft reports, etc. are used as observational values. If there are reliable observations, the first-guess value estimated by the GCM would be almost replaced by this observational data. However, these values are always dominated by GCM forecasts in regions with sparse observation.
The physical parameters of
(geopotential height),
(wind velocity E-W),
(wind velocity N-S),
(vertical pressure velocity),
(temperature), and
(relative humidity)
are located at each 2.5 degree grid point,
they cover the globe by 144x73 matrix.
There are seven layers at 1,000, 850, 700, 500, 300, 200, and 100 hPa
heights and values are defined on these levels.
Data archives are available after the First GARP Global Experiment
(FGGE) in the year of 1979. FGGE was the first opportunity
for such a numerical weather forecasting center to develop
the four dimensional data assimilation system in practice.
Twice daily data are used in this study,
because there are mainly twice daily observations by atmospheric soundings,
even though ECMWF have made intermittent 6-hour
analysis-initialization-forecast cycles.
The algorithm used in this study
to estimate the by equations
(2), (3),
and (5) from ECMWF data set
is described in the remaining part of this section.
Different algorithms may be required for different data sources
in order to implement the atmospheric water balance method.
If the surface pressure is below 1,000 hPa, and sometimes below 850/700 hPa in mountainous regions, these levels locate below the ground surface in reality. However, extrapolated values are stored at these pressure levels in the datasets used in this study, and no information is provided for the values at the ground surface. Surface pressure is necessary for the vertical integration, and it requires a computation similar to that used for the reduction to mean sea level;
[Cdeg.]) and pressure height (
[gpm])
at the lowest level of the data.
The equation is:
where 
[m]
is the altitude at that grid, and
adiabatic temperature lapse rate 
is
set to 0.005[deg.C/m].
,
therefore a temperature correction factor
is computed as
Then the corrected mean temperature
[K] is computed from
the equation 
.
is given
using the lowest pressure 
,
gas constant 
(=287.05 [m^2/s^2 K]),
and the gravity constant
(=9.80 [m/s^2]):
Physical parameters at the ground surface
,
such as pressure, temperature, etc.,
are interpolated using values
and
at the levels of 
and
(
).
The values =1000 [hPa] and
=850 [hPa] are used for extrapolation
in the case of 
[hPa].
Logarithmic values of pressure are used for interpolation (or extrapolation).
The equation is
Specific humidity can be computed using the pressure
,
temperature [K],
and relative humidity [%],
according to the equation:
where 
(
) is the ratio of the density
between dry air and the water vapor.
Saturated vapor pressure 
[hPa]
at temperature [K]
is calculated using Goff-Gratch's equation
[Goff and Gratch, 1946]:
(=273.16 [K])
is the triple equilibrium temperature of water,
and the saturated vapor pressure for liquid water surface is also used
in the case of 
[deg.C] =273.15 [K].
The vertical integration of 
is
computed as 
.
The thickness of the layer 
is given by
The components of the 2-dimensional vapor flux
,
and
are
similarly computed.
In the discrete equation, the convergence
at latitude of 
and longitude of 
is computed using the centered difference approximation:
Vapor flux convergence is given with the dimensions of [kg/m s], and is converted into [mm/s] by assuming the density of water to be 1.0, which simplifies the comparison with annual runoff.
These data processing steps are made for each twice daily data sets,
and monthly and annual mean value are integrated from
these twice daily estimates of
,
and
.
The sampling effect on these estimates are
discussed by Phillips[1992],
and the diurnal variation, especially in tropical area,
is very large [Oki1994a].
However no detailed discussion is made in this paper on these questions.
The vertically integrated atmospheric water vapor
flux and the precipitable water in an atmospheric column are shown
in Fig. 2 for annual mean,
Fig. 3 for January and
Fig. 4 for July.
The arrows show the direction and the strength of vertically
integrated vapor flux, and the shading indicates the precipitable water.
For the sake of consistency,
these figures are displayed as
the four years mean from 1985 to 1988.
Precipitable water
is essentially described by the surface temperature,
and its distribution is more or less symmetric with respect to the equator,
and it moves
north and south according to the seasonal march of temperature.
The vertical contour lines, which can be seen in the southern Pacific Ocean
for a year and in the northern Pacific and Atlantic Oceans in July,
indicate strong mixing or transport of water vapor in the
north-south direction.
The difference between the land and ocean is significant,
and is small
over continents except for the Amazon River basin and south-east Asia.
The vapor transport occurs mainly over the oceans,
but in the Amazon basin in January,
and the Asian monsoon system from Madagascar, Somalia Peninsula, Arabian Sea,
Bay of Bengal to East China Sea in July, carry significant vapor water fluxes.
The effect of monsoon is difficult
to see on annual average plots because the summer (July)
south-west monsoon and winter (January) north-east monsoon nearly cancel.
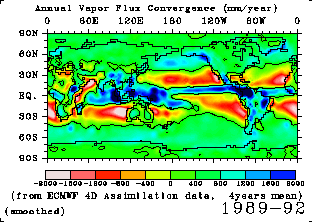
Flux convergences are shown from Fig. 5 to
Fig. 7
for the annual mean, January and July respectively.
The mean over the globe,
which theoretically should be 0, was approximately 0.07 mm/year.
The negative region indicates
annual evaporation exceeds
annual precipitation (see eq.(10)).
Such a situation over land may occur at some part of an inland river basin
or at the lower part of a large river.
Almost every negative estimated
values fall in such regions.
However, Masuda Masuda1988b pointed out that
the observations at points surrounding arid areas may cause
an increase of vapor divergence (negative convergence).
The improvement in data analysis techniques may eliminate
the negative annual convergence regions over land.
Tropical regions and mid- and high-latitudes are convergence zones globally. The tropical convergence zone from the Indian Ocean to the west Pacific Ocean is wider than any other. The high convergence regions generally correspond to the region of high precipitable water, however, the convergence zone at the northern ends of the Pacific and Atlantic Oceans do not have high precipitable water. The polar frontal low depression tends to grow in these areas. Sub-tropical oceans are generally regions of divergence, but parts of them represent negative divergence zones at the so-called South Pacific Convergence Zone, at the offshore of eastern Australia in January, and in Asian monsoon convergence zone at the west Pacific Ocean in July.
The GEWEX Asian Monsoon Experiment (GAME) has been proposed as a part of the Global Energy and Water cycle Experiment (GEWEX) under the World Climate Research Programme (WCRP). Process studies are one component in GAME, and four regions are planned to be intensively investigated. They are Siberia (Taiga/Tundra), Tibetan Plateau, sub-tropical/temperate monsoon region (Yantze, Huai-He and Huang River, China), and the tropical monsoon region. In this regional study of GAME in tropics, Chao Phraya river basin is selected for the water balance study and macro-scale hydrological modelling.
The Chao Phraya River flows through the center of Thailand, and its catchment area is about 178,000 km^2. From the global point of view, this size is not large (Fig.8).
Discharge data used here were provided by the Electricity Generating Authority of Thailand(EGAT). The first data set is inflow to the Bhumibol dam at Ping river, which is a tributary running through north-western part of the basin. Another is the inflow to the Sirikit dam at Nan river, which is also a tributary within the north-eastern portion. Discharge data observed by the Royal Irrigation Department (RID) was also used. Station P.1 is located upstream of the Ping river. As an index of the total discharge from Chao Phraya river, observations at station C.2 was also used, which is located downstream of the confluence of four main tributaries, but before Chao Phraya river divides into several channels running through its delta. Catchment area at each station point is shown in Table 1. Rainfall data were observed by the Thai Meteorological Department, and the arithmetic means of the data at each station in the catchment area were used.
Estimated annual atmospheric water vapor flux convergence
(i.e. the arithmetic mean of surrounding 5x5 grid points,
at 2.5 degree resolution of 95-105 E and 12.5-22.5N),
annual discharge, and annual precipitation are shown
in Fig.9.
Annual change of water storage both in the catchment
(
)
and in the atmosphere (
)
are comparatively negligible.
Therefore the annual vapor flux convergence should match the annual
discharge from equation (10).
However the quantitative agreement is not perfect.
One main reason is that
this basin is surrounded by mountains except in the southern direction.
The basin is shielded by both the south-west
and north-east monsoons, and has less water vapor convergence
compared to the surrounding regions which are wind-ward of the monsoons.
Regions on the wind-ward side are known to have more rainfall
[Oki et al.1991],
but evapotranspiration may differ less.
Consequently, the actual convergence value in the basin should be
much less than the value estimated here, which is the mean of 25 grid points,
10x10 degree area.
The annual precipitation map clearly indicates
such a distribution of moisture convergence.
An apparent gap can be seen in
between the year of 1984 and 1985
(Figure 9).
There were some significant changes in the data analysis system/algorithm of
ECMWF during this period, especially regarding
the GCM spatial resolution, treatment of cloud and
water vapor parameterizations [Hoskins 1989].
Because products of later years are expected to be improved,
the data after 1985 are used in this study.
Even though the absolute value does not give good results,
the temporal variation is very similar between
vapor flux convergence and observed discharge.
In order to clarify this point, a reduction factor
was applied to the mean
of every month during 1985-1988.
A value of
was chosen such that the 4-years total
will
agree with the corresponding observational discharge at Bhumibol Dam.
Rasmusson [1968] found a net increase in storage of 210 mm
within 5 years over continental US,
and he corrected
by the uniform addition of 3.5 mm/month.
The development of a coherent correction method is
beyond the scope of this paper.
In any case, this rough correction should be replaced in the future when more
temporally and spatially resolved data sets could be obtained.
Corrected monthly net water vapor
convergence(
)
is calculated, and a comparison with the observed monthly runoff is shown
in Fig.10.
The time variations agree very well, and it is concluded that inclusion
of a correction factor provides a better estimation for the case under study.
The temporal change of storage
is neglected in equation (10)
for annual water balance, but it cannot be neglected for the monthly
water budget and the storage may make the discharge appear delayed compared
to . Approximately one month of
delay can be seen in Fig.10,
for this case.
By applying the atmospheric water balance method,
storage can be estimated
using observed discharge data (equation 12),
and evapotranspiration can be estimated using observed precipitation data
(equation 11).
Fig.11 shows the change of total water storage
in the Chao Phraya river basin.
Discharge and precipitation are from surface observations.
Corrected is used
and the initial storage is set to 0.
In 1986, the precipitation is similar to the other years but
the basin storage
is estimated to be less than in other years.
The discharge is also less than in other years and it certainly reflects the
shortage of basin storage .
On the other hand, the basin storage and river discharge are
comparatively high in 1985.
Note that the seasonal change is much larger than the intra-annual
variation. Storage value recovers close to zero at the beginning of
each year.
It supports the assumption of 
0
for the annual water balance.
Fig. 12 shows the estimated evapotranspiration values by
atmospheric water balance, Penman equation, and model output of
the ECMWF-GCM given in the TOGA-COARE CD-ROM
[Oki and Sumi 1993].
The original spatial resolution of the ECMWF data in TOGA-COARE CD-ROM
was 2.5 degree, and it is integrated over the 10x10 degree region
corresponding to the estimated .
Penman evapotranspiration has its maximum in March and April, the
ECMWF model evapotranspiration has its peak in August, and the
evapotranspiration from atmospheric water balance
has a very similar seasonal change to
precipitation. Penman evapotranspiration would only represent a potential
value and it is not realistic because there should be limits to the
water availability
for evapotranspiration at the end of dry season in March to April.
ECMWF model output
has small seasonal variation compared to the atmospheric water balance
estimation, the reason could be that 10x10 degree region contains
the sea surface evaporation.
Atmospheric water balance estimates,
on the other hand, show negative evapotranspiration at the end of
1986;
the true value for evapotranspiration is expected to be between
the ECMWF model output and atmospheric water balance estimation.
For improved understanding of the large scale patterns of evapotranspiration,
intensive observations are inevitably required especially in the dry season.
Therefore,
one of the main issues
in the intensive field observation within the Chao Phraya River Basin
under GAME is :
Even though the quantitative correspondence between
and
discharge is not perfect, corrected
seems adequate for understanding
the basic hydrological cycle in the Chao Phraya River basin.
The atmospheric water balance method gives valuable information
about the water balance within a river basin, such as the large-scale
monthly evaporation and the seasonal change of basin storage.
This information is especially helpful in regions of sparse observation
in the tropics [Matsuyama et al.1994]
[Matsuyama 1992].
Annual vapor flux convergence is summarized in each of 70 river basins and compared with mean annual runoff (Table 2). River runoff observed at gauging stations is from the Global Runoff Data Centre [GRDC1992] and also from UNESCO [1969]. Long term mean values are calculated from these data by averaging over available data period in each station. Seventy rivers which have basin areas greater than approximately 100,000 km^2 were selected. The continental land mass was divided into river basins manually using published world maps in 2.5 degree grids. In the Table 2, the atmospheric vapor convergence to the Chao Phraya river basin is estimated from only three grids instead of surrounding 25 grids.
Normalizing for basin area, the mean
in these 70 rivers is approximately 220 mm/year.
The size of the river basin is considered in the averaging procedure.
This value is larger than that for whole continents
(i.e. 165 mm/year in Table 4),
but it is smaller than the mean observed runoff of these specific rivers,
which is 314 [mm/year] according to GRDC,
and 365 [mm/year] according to UNESCO.
These 70 river basins cover only 55% of the land surface of the earth,
yet they hold 75% of total
within land and their mean runoff is larger than the global average,
indicating that
the areas where large rivers exist have comparatively high runoff rates.
It suggests the global water balance estimated by the extrapolation of the
large river water balance may overestimate the true global value
for the continents.
Comparison with observed river runoff is
shown in Fig. 13 based on the absolute difference
between the two data sets.
The tendency is not clear but larger river basins have smaller differences
between and observed runoff.
The tends to be smaller than
the corresponding river runoff (Table 2),
and it may be caused by the weak divergence of the wind in the ECMWF
objective analysis data set [Masuda 1988b].
If the estimation error is evaluated by the ratio of predicted to observed value (as seen in the last column of Table 2), the ratio of the error (expected to be zero) is within the range of +-1.0 in 34 rivers among the 68 rivers of comparison. Due to the lack of the discharge data, no comparison was made for Tegwani and Yana rivers. The major difficulties confronted in the comparison of atmospheric vapor convergence and river runoff here are:
itself seems to be erroneous in these mountainous areas
because of the representation of topography in the
data assimilation system.
= 0. Inter-annual variation of the
soil moisture storage will cause the difference.
The observed runoff may be influenced by human activities, such as the intake for an irrigation scheme or the storage in a reservoir. However, such an effect should appear in a similar manner in the results of the atmospheric water balance method. Therefore, anthropogenic effect will not be the cause of any error. In the case of hydrologic simulations which do not incorporate the human activities, numerical models may predict a different result from that of the atmospheric water balance method as well as observed runoff.
The geographical distribution of the absolute differences
between predicted mean convergence and observed runoff
are shown in Fig.14.
The poor correspondence occurs in the South Africa,
the Central and Monsoon Asia, and the South America.
These areas have extremely few observational points
or large amount of precipitation.
On the contrary, there are many basins that show good correspondence
(the absolute difference is less than 150 mm/year)
in the mid- and high-latitude regions of the northern hemisphere.
The error index ratio from Table 2 also has a similar
geographical distribution.
This distribution may reflect the high quality and high density
of the observations, especially with respect to the atmosphere,
which underscores the importance of actual observations in order to perform
accurate data assimilations.
Fig. 15 shows the zonal (east-west direction) mean of vapor flux convergence, and the comparison with prior results [Baumgartner and Reichel 1975] of the latitudinal distribution of precipitation minus evaporation. The two methods generally show good agreement quantitatively. However, the results of this study show that evaporation excess over precipitation is greater than the result by Baumgartner and Reichel [1975] at sub-tropical latitudes.
Global annual runoff from whole continents is calculated using the land-sea distribution (Fig. 16). Table 3 and Table 4 show the comparison with available estimates. Baumgartner and Reichel [1975], Lvovitch [1973] and Korzun[1978] estimated runoff by hydrological methods using surface observations. Bryan and Oort [1984], Masuda Masuda1988b and this study used the atmospheric water balance method. Note that the Middle East is included in Europe, not in Asia, and the Arctic Ocean is included in the Atlantic Ocean in the Bryan and Oort Bryan1984 estimates.
The results of the present study are comparable to those of FGGE-ECMWF [Masuda1988b], but appear to be relatively small compared with results of basin water balance analyses as with the values presented by Bryan and Oort Bryan1984. According to Korzun [1978], land cover on the earth is approximately 29%, but 31% was assumed in the topographical model employed in this study, and this may underestimate the mean convergence over land.
The signs of
in Table 3 are almost the same
among the estimates, but the absolute values vary.
In the Pacific Ocean, the precipitation and evaporation approximately
balance each other,
evaporation exceeds precipitation in the Atlantic and the Indian
Oceans, and vice versa in the Arctic Ocean.
In Table 4, results from hydrological method produce similar estimates, and the results by the atmospheric water balance method generate smaller values than the hydrological estimates except for Africa and South America (i.e.
