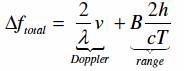MRRの新しいマニュアル（ver.1.8.4）

1. MRRの特性

1.1. 概要

1.2. レーダ周波数

1.3. レーダの入出力

1.4. FM-CW形式

1.4.1. 静止している観測対象

1.4.2. 距離分解能

1.4.3. 移動する観測対象

移動する対象からのエコーはさらに位相を変化させる。この変化量はドップラー効果によって速度に比例している。

したがって、距離の違いによる位相変化と、速度による位相変化には「あいまいさ」が、あるように思われる。実際、この「あいまいさ」は、一つのレーダで観測している限り、切り分けることができない。したがって、FFTの周波数分解能が1/Tであり、隣接する周波数との間にはFFT線が存在しない。一回の走査の間で観測される周波数のずれは数式 1.4.3.2のようになる。

数式 1.4.3.1

われわれは、図 1に示すような、レーダの走査で「ゆっくり」動く対象からのエコーを考えている。それぞれのレーダ走査による信号波(Beat signal)はフーリエ変形(第1次FT)の結果である。なお、複素スペクトル線を極座標系で矢印を用いて示している。個々のスペクトル線はひとつのレンジ区間(距離幅)rを示している。図 1にはレーダ近傍の10個のレンジ区間を示す(0≦r≦9)。MRRでは32個のレンジ幅を計算している。ここで、観測対象はレンジ番号3と4の間に位置しているのでスペクトル強度は3と4に等しく配分されている。

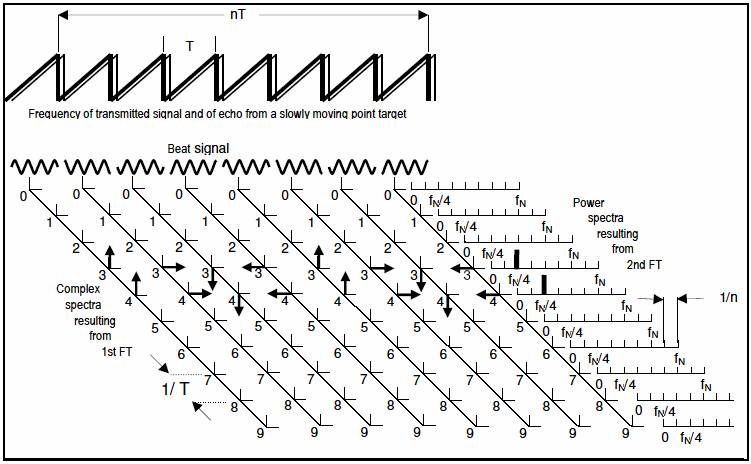
図 1　ゆっくり動く対象からのエコーの模式図
エコーの時間・空間領域を示す。

この例では次の式で示される速度でレーダに近づいている。

数式 1.4.3.2

すなわち、観測対象の位置はある時刻のレーダ走査から次の操作の間に、λ/8だけ移動する。この距離はレンジ幅の深さに比べると小さいので、対象の位置はやはりレンジ番号3と4の間にあり、エコーの位相は次の走査までに90度進む。　3/7’6

ここで、それぞれのレンジ区間にある電圧の複素スペクトルを新たな時系列として解釈する。時系列のサンプル間隔は1/Tである。この時系列のフーリエ変換は分解能が1/nTであるパワースペクトルを作る。この2番目のFTにおいて、あいまいさのない周波数範囲(ナイキストレンジ)は周波数間隔がｆN=1/Tである波で構成される。ここでの例では、最大の周波数スペクトルはレンジ番号３、４で周波数が以下の式のところに現れる。(4/24’6)

数式 1.4.3.2

数式 1.4.3.2と数式 1.4.3.2を比較すると、fD＝2ν/λであることがわかる。これはまさにドップラー速度の関係である。2次のフーリエ変換で得られるスペクトルは対応するレンジ区間でのドップラー速度と解釈できる。

距離と速度を分割することは対象物の速度のあいまいさがナイキスト間隔に納まる場合に限られる。落下する雨滴の場合は、正のシフトを仮定している。したがって、周波数が0≦ｆD＜ｆNの範囲であれば、あいまいでなはい。ナイキスト間隔の幅は、走査線の繰り返し比１／Ｔを選択することによって調整できる。(4/25’6)

1.5　スペクトルの処理

1.5.1 位相がそろっていない平均(Incoherent Averaging)

散乱体積内に、無作為(random)に分布している、多数の標的から得られた信号のスペクトル強度(spectral power)は、全要素の任意の位相で重ねられた、大きな統計的な(stochastic)成分を含んでいる。おおむね（incident 起こりやすい、ありがちである）、観測した強度(power)の標準偏差は、強度の真値(expectation,期待される値)に等しい。したがって、強度スペクトルの集団(ensemble)で平均することで統計的な成分を減らすことができる。強度スペクトルをｎで平均すると、nが1より十分大きいときに標準偏差を1/√ｎだけ、減らすことができる。2/23’6

MRRのDSP(ドップラースペクトルプロセス?) は1秒で25のスペクトルを作り、これは実時間の80%である。(n=25であるので√n=5、1/√n=0.8)。標準の設定では、DSPは10秒ごとに平均したスペクトルを受信系に伝送する。データ転送は約4秒必要である。この間は観測ができない。したがって、正味の平均間隔は6秒であり、6秒間には150個の単一パワースペクトル（single power spectra）が含まれる。この結果、(n=150で1/√n=0.08)スペクトルの統計的な標準偏差は、8%あるいは0.34dBに抑えられている。3/2’6

今、我々は、新しい観測値で各レンジ幅において、電力の複素スペクトルを1/Tごとに解析する。この時刻の観測でそれぞれのフーリエ変換は1/nTの解像度でスペクトル強度を生み出す。明確な周波数範囲(ナイキスト範囲)の第2FTはｆN=1/Tで構成される。我々の例でスペクトル強度の最大は、ゲート3と4の強度に見ることができる。3/9’6

1.5.2 雑音(ノイズ)の評価について

エコーの信号に加えて、避けることのできない雑音(ノイズ)がレーダの受信機に入ってくる。この雑音を除くことができれば、見掛けの雨量を検出できる。偽の雨量は小さいかもしれないが、雑音があることで積算雨量には重大なバイアスが生じるかもしれない。(実際の雨量は観測時間の数%のみ発生し、季候区分や季節に依存する)

そこで、ノイズの評価手法を信号解析手順に組み込んでいる。この目的のため、雑音の特性を、「信号から分離可能である」と仮定している。さらに、雑音は解析するドップラ範囲では「白色」(周波数依存がない)と仮定している。信号と同様に、スペクトルの雑音強度は、これまでに述べた設定では統計的に信号の8%あるいは0.34dBに等しい変動を示す。(4/26’6)

ノイズの評価は次の手法による

１．スペクトルの平均を元に、S/N(基準値)を設定する。

２．最大のスペクトルを除き、スペクトルを計算する。

３．スペクトルの平均値が、前の値と同じか、大きくなった場合に、スペクトルの平均値をノイズレベルとする。

模式図を図 2に示す。

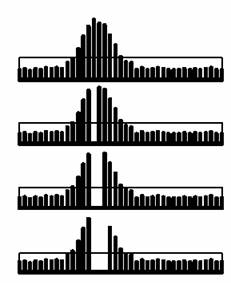
繰り返す　↓

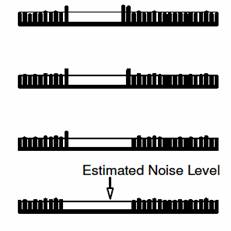
図 2　ノイズの評価方法
細い線は残ったスペクトルの平均値を示す。

2. 落下粒子の粒径分布の計算

レーダで得られるスペクトルパワーは、下記で表現される。

　　　　　　　　　　　　　　　　　　　　（2.1）

はレンジ（高度）分解能、はレンジゲート番号、はレーダの特性パラメータを含む、補正係数で、レーダ特性パラメータには、送信出力、アンテナの利得、（周波数に依存する）MRR受信機の導波管関数が含まれる。は空間反射密度、すなわち、体積当り、周波数あたりの後方散乱断面積である。は2回目のフーリエ解析の周波数解である。は、補正係数がわかっていれば、生のスペクトルから求めることができる。