0601

ドップラーレーダを用いた雨雪判別の文献調査

査読者が指摘する文献をレビューする。

 

検索：

Words from Abstract (ALL) : classification rain snow radar

 

Search Results: Articles Found: (1 - 3 of 3)

[Abstract] [Full-text Article] [Print Version]

急速に発達した強風雨(ストーム)を2事例、局地爆風・暴風雷雨(マイクロバースト・シビアサンダーストーム、1986)計画において解析した。それらは、急速に発達した雹を伴っている。1986年7月20日の事例はよく調査されている、単一セルの風雨である。もうひとつは同年7月6日の事例であり、マルチセルの風雨に含まれるひとつのセルである。両者とも10分間で雹を生み出すような､効率のよい付着成長(accretion)の例である(併合成長(coalescence)は、雲粒の成長に使い分ける予定)。降水粒子の判定には、7月20日の事例を元にしたアルゴリズム(別の著者による)を、7月6日の事例に当てはめた。

 

雹と霰を発生させる雲物理の発達過程は2つの風雨で類似している。雲水量が大きい、上昇流の中での急速な雲粒の併合成長により、雲粒が降水粒子サイズまで成長した。この粒子は0℃高度より上空に運ばれ、凍雨となる。これらの凍った粒子が霰や雹の種(embryo)となり、付着成長で成長を続ける。過冷却の雨滴はセルが発達する8-12分間のほんの初期にだけ存在し、0℃高度上空1-2kmの高さに広がっている。霰や雹は最初に過冷却の雨が降ってから数分後に出現する。霰は雹よりも高い高度、大きい領域を取り囲んでいる。過冷却の雨が氷晶化を終える(completion)タイミング(水がなくなる時)と、霰と雹の落下が始まるタイミングはほぼ同時である。(1/12’6追記)

 

霰や雹を生み出すような風雨は、雨だけを生み出す風より自らの寿命を縮めてしまう(1･11’6)

 

[Abstract] [Print Version]

[Abstract] [Full-text Article] [Print Version]

 

Words from Abstract (ALL) : classification radar

では66件ヒット。Bringさん、Zrnicさんらの最近の研究がヒットする。

そのものずばりはヒットしない。

分類の文献をレビューし、引用文献を確認する。1/11’6

 

Radar Observation of the Atmosphere Louis J. Battan　https://opac.dl.itc.u-tokyo.ac.jp/opac/books-query?mode=2&code=21549979&key=B114714791914074

8. パルスドップラーレーダ

8.5       ドップラースペクトルの幅

ドップラースペクトルはさまざまな原因により広がりを持つ。

１．粒径分布の広さ
大きい粒子が存在するとスペクトルの分布は広くなる

２．大気の乱流スペクトル

３．風の鉛直シア

４．観測ビーム内で大気の運動が一定でないこと

 

 

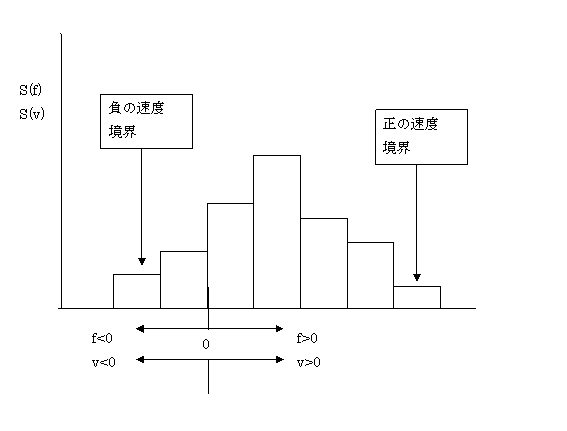
スペクトルの幅は簡単に求めるは、ノイズレベル以上の信号が得られたドップラー周波数の「最大値―最小値」で求めることができる。より、便利な方法はスペクトルの分散で定義する方法である。必ずしも、スペクトルの分布がガウス分布にならないが、分散はよい指標である。分散を求めるためにまず、平均を計算する。

 

　　(8.18)

 

この表現は、後方散乱強度で重みをつけた平均速度を与える。4/12’6

粒径分布がわかっており直径の関数として粒子の落下速度が表現できると、静止大気中の落下速度は反射因子を置き換えることで計算できる。

ドップラースペクトルの分散は次の式で得ることができる。

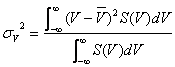　　(8.19)

5/9’6

を計算する場合、結果は、測定される後方散乱強度の表現によらない。表現は、S(V)、レーダ反射強度η、後方散乱断面積σ、レーダ反射強度因子Zがある。

 

 

表8.2

アンテナが直上を向いている時、静止大気中を落下する降水粒子タイプごとのドップラー速度スペクトルの分散

 

降水粒子タイプ

 

 

雪

0.04-0.3m2/sec2

Hitschfeld and Dennis(1956); Lhermitte(1962);Rogers and Tripp(1964)

融解中の雪

0.5m2/sec2

Lhermitte(1963b)

雨

0.7-1.6m2/sec2

Lhermitte(1962,1963b)

霰(氷相)−最大粒径

乾いた霰

湿った霰

Boston and Rogers(1969); Donaldson and Wexler(1969);Battan and Theiss(1968)

2cm

8m2/sec2

5m2/sec2

4cm

24m2/sec2

8m2/sec2

5/11’6

Hitschfeld and Dennis(1956)は全体の分散σv^2が4つの要素(パワー、η、σ、Z)の和で書ける事を示した。散乱体が一様な動きでレーダビームを横切る効果は、風が強くビームが狭くない場合に重要となってくる。

しかし、1°より小さければ、この効果は無視できる。

風のシアの効果もビーム幅による。Lhermitte(1963b)、SLoss and Atlas(1968)、Atlas,Srivastava,andSloss(1969)によって調べられている。ビームを横切る方向の風のシアがスペクトルに与える影響は、ビーム幅が1°より小さい場合は無視できるほど小さい。ビーム幅が2°に近づくにつれて測定される変動は数十kmより長い距離で重要となってくる。

アンテナが鉛直向きでビーム幅がおよそ1°の場合、落下速度と擾乱の大きさで決まってくる。5/12’6

 

8.6       信号の変動

時刻tとt＋τにおけるビデオ出力の相関係数を取ることで、擾乱の時間依存性を調べた。

 

R-meterというものの原理は、大気中の擾乱の下向き運動と上向き運動の組を何回横切るかである。

 

8.7       擾乱の測定

表8.2は、降水粒子が静止大気中を落下するときに、ドップラースペクトルの分散がどの程度変動するか、を示している。スペクトルの分散は明らかに、、散乱体の配置、および、落下速度に依存している。

 

8.8       上昇流の測定

パルスドップラーレーダでは、アンテナを鉛直に向けると対流性の雲の上昇流を推定できる。

Probert-Jones and Harper(1961)は最初に、鉛直流のパタンを示した。0℃高度より上で、雪は探知可能であると仮定している。そこで、負の値は地面に対する氷粒子の速度と仮定している。粒子の終端速度と考えられる1m/sを加えることで、鉛直流の大きさを評価した。0℃高度より下の鉛直流を評価するためにProbert-Jones and Harper(1961)は次の仮定を用いている。

(1)   鉛直速度は融解層を通じても連続している。

(2)   融解層の底から地面まで、大粒子の終端速度は変化しない。(5/15’6)

 

この仮定に基づいて、大気の速度の変化を雲の高度の関数として推定する。この手法は、雨域における大気速度を評価する。

Battan(1964)、Battan and Theiss(1966)はProbert-Jones and Harper(1961)の手法を拡張した。彼らは、シャワーのたいていの場所で落下速度1m/sの粒子が存在する、と仮定した。0℃高度より上では、粒子は凍っている可能性があり、下では、小粒子の雨は散乱している。降水粒子の気柱の全体の深さをつうじて、ドップラー速度1m/sを加えた、負の速度(最大上昇流)の領域は鉛直速度と考えた。ATLAS(1964)はこの手法はシャワーの端では誤差が起こると指摘している。降水粒子の分類が起きているので（驟雨の始まりは大粒子が多い、の意か？）。5/16’6

負のドップラースペクトルが有効であるかどうかは、重要要素(crucial factor, テクニカルタームかもしれない)の数による。ゆっくり落下する散乱粒子の存在が必要であり、検知可能であり、粒子の終端速度がありえる値として算出されることが必要である。

粒子サイズのスペクトルが幅広の場合には、小さくて検知不可能な粒径から検知可能な粒径まで、粒径が分布していると仮定してもよい。Marshall and Palmer(1948)はこの描写を満足している。(指数分布で表現すると粒径が小さいところに、数濃度の大きな値が表現される。このことの正当化か?)

幅の広いスペクトルがある場合には、大気の運動を予測精度は検知できる最小粒径に依存する。典型的なXバンドレーダでは、0.2-0.3mmの粒子が探知可能である。最大の範囲は普通10kmより小さい。探知できる粒子の終端速度は1m/sもあると考えてもよいであろう(5/17’6)

 

 

終端速度Wは粒子の粒径に関係している。粒子の粒径はZに関連していることからZとWの関係式を見つけることができる。

Roger(1964)は

(1)   レーリー近似が成り立つ

(2)   粒径分布はMP分布(ND=N0*exp(-ΛD) )で表現できる。

(3)   終端速度はSpilhaus(1948)で単一に決まる(Wt=K*D^0.5)。

を仮定してドップラー速度Vと反射強度因子Zから鉛直速度を求める手法を提案した。

 

W=3.8 * Z^0.071　(8.26)

Zが大きいと、Wが大きくなる。

下降流については

Wa=V-W　　　　　　　　　　　(8.27)

で評価できる。Vはレーダで観測される下向き正の風。例えばV=-9m/s(上向き9m/s)のとき、ZからW=5m/sが見積もられたならば、Wa=-14m/sとなる。つまり14m/sの上昇流となる。

Rogerは彼の手法に不確実な点があることを認めていたが、雨が対象の場合には上昇流は1m/s程度であろうと述べている。

 

 

 

地形の影響による台風7002号の降雨量のmodification

http://www.mri-jma.go.jp/Project/mrinpd/CORPJ.htm( 関連が高い)

Sakakibara and Takeda(1973)

実施にk(X,Y)が地形、環境の風のみによって決まっているのであれば、全降雨の分布は雨量分布を長期的に平均することで得られる。

4/17’6

実際に降った雨R(x,y,t)を地形性の雨g(x,y,t)と擾乱による雨f(x,y,t)に分割して考える。

擾乱による雨は観測点周辺の地形、一般場の風向風速により、強化されていると考える。したがって次式が成り立つと仮定する。

R(x,y,t) = k(x,y)×f(x,y,t) ＋ g(x,y,t)      …(2)

g(x,y,t)は10mmを超えるような雨の場合は、擾乱による雨に比べて小さいとみなせるので、この解析では無視する。

 

R(x,y,t) = k(x,y) × f(x,y,t)              ...(3)

5/10’6

k(x,y)とはある期間τの間は、時間によらず一定値である、と考えられる。ある期間τの間は一般場があまり変化しない。特に、風向について変化しない。そこで、R(x,y,t)を｛R(x,y,t)｝で割ることでR(x,y,t)からk(x、y)を取り除くことができる。｛R(x,y,t)｝は時間平均を表す。

 

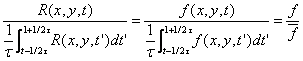　　(4)

 

図6は(おそらく)図5とリンクしている。図5は「山地部の雨量は平地の雨量より格段に多い」ことを示す。

また、「f(x、y、t)は擾乱本来の雨」であり、増幅の結果山地部のほうが雨量が多いが降雨のパタンは同じである。。

 

ここでf(x,y,t)/{f(x,y,t)}をh(x,y,t)であらわす。{f(x,y,t)}は、擾乱が移動する方向に沿って存在する、異なる雨量計で同じ値となる。ただし、τは十分長くて、擾乱は半島を通過する際に、発達も消失もしない、と考えている。

 

図12

地点間におけるｈの定量的な差はfの値そのものが地点で変わることを意味する。

 

地形がなかった場合に擾乱がもたらす雨量f(x,y,t)は、擾乱の進行方向をX、進行方向と垂直にY軸を取り、Y軸方向には一様と仮定する。

その結果、各地点での雨量は

R(X,Y,t)=k(X,Y)×ｆ（X-Vt）

と表現できる。

 

ここで、計算している時間はｆを一定としていることから2点間で、ある期間は変化しないと仮定している。

⇒2点間の比を取っていけば、増幅係数k(x、y)はある程度推定できる。

 

増幅係数がわかれば、地形の影響がないとした場合の雨量を計算できる。11/30’6