�������̐ᗱ�q�̊O�C�Ƃ̔M�����ɂ���
2/14�f8�@�z�c
1. ���Ƃ̗\�f���ɂ�����Z���̎�舵���ɂ���
�Ì��ߒ��́u�i�q�X�P�[���v�Ɓu�ω_�Η��v�ɕ����Čv�Z�B�Ì������_�ɂȂ��Ă���킯�ł͂Ȃ�(H7�e�L�X�gp67)
���Ƃł͐ᐅ��(�~���cm/�~����mm)��\��iH9�e�L�X�gp28�j
�C�ے��\�e�L�X�g�ɂ͗Z���ɂ��Ă̋L�q�͂Ȃ��B
2. �Z���ߒ��̎�舵��(�ЂƂ̗��q�ɂ���)���g�m�[�gp84
2-1. �O�C����̔M�ɂ�闱�q�Z���̎�
2-1-1. �l������M
�X���q�̗Z���ɂ��Ă͈ȉ���2�̔M���l������B
�P�D�O�C����̔M�`��
�Q�D���ω��̐��M
2-1-2. ���_�I�ȔM�̗A����
���������ł͐��H�A蹂����`�Ƃ݂Ȃ��ē`�M���_�̉��p�Ƃ��Ď�����������W�������߂Ă���[1]�B�O�C����X�\�ʂւ̔M�t���b�N�X�͈ȉ��̎��ɂ��B��P�����M�`���A��Q�������ω��������B�S��R�Ȃ̂ŁA�C���ɒ��s����f�ʐϐ�����ΏۂƂ��Ă���B
![]()
R�f:�X���̔��a
K:��C�̔M�`����
��T�F�X���ƕX������\�����ꂽ�ꏊ�̊O�C�Ƃ̉��x��
Lv�F���̏����̐��M
D�F��C���ɂ����鐅���C�̊g�U�W��
���ЁF���̕\�ʂƕ\������\�����ꂽ�Ƃ���̊O�C�Ƃ̐����C���x��
�W��a�͔M�A���̒ʕ�(ventilation)�W���ł���B���S�ȋ��̏ꍇ�AYuge[2]�̎����ɂ����C�m���Y����10�`1800�̊Ԃɂ����Ď����ŕ\�����B
![]()
������Pr�̓v�����g����(���S�x�k���̓��̔S��̓x�����l�Ɖ��x�g�U�̔�)�ARe�̓��C�m���Y���������B
�����C�̒ʕ��W���͔M�A���Ɠ����`�����肵�Ď����ŗ^����B
![]()
�����ŁASc�̓V���~�b�g��(���̂ɂ����铮�S�x�Ɖ��x�g�U�̔�)�ł���B��C�̃v�����g�����A�V���~�b�g���͒ʏ�0.71��0.60�ł���̂ŁAPr^(1/3)=0.892�ASc^(1/3)=0.8434�ł���قړ����l�ƂȂ�̂ŁA�����i1984�j�ł͂Ƃ���0.87��p���Ă���B���������āAa�Ab�͂Ƃ��Ɏ����ŕ\�������B
![]()
2-1-3. ��Ђ̌`�̌���
��̕\�ʂ̉��ʁA���E�I������\�����߂ɁA��Ђɑ���M�A����H�A�X���ɑ���M�̗A����H�f�Ƃ��ĕ���l����B�M�`���ɂ��M�A���A�����C�ɂ����M�A���̕����ߒ����ގ����Ă��邱�Ƃ��l����ƁA��Ђ̌`�ɂ��M�A���̌W��(��l)�͔M�A���ƁA�����C�A���ł���قLj��Ȃ��ƍl������B���������ĂЂƂ̒����W���Â�p���Ď��̂悤�Ɏ�舵���B
![]()
�����ŁAR�͐�Ђ����Ɖ��肵���Ƃ��̋��̔��a�������B�Â͐�Ђ̌`���`�łȂ����Ƃɂ�钲���W���ł���A�P�ʖʐς�����̌W���Ƃ��čl���Ă���B���߂Ŏ��������ɂ�苁�߂��l�𗘗p����B
2-1-4. �����W���̒���
1) �Z�𒆂̗��q���̉��x���z
�Z�𒆂̐ᗱ�q���̉��x���z�́A�ȉ��̗��R�����l��0���Ƌߎ�����B
�E ���̔M�`�����͋�C���傫���A���q���̔M�̗A���͊O�C����̗A���ɔ�ׂđ����B���������āA�M�͐�����0���̕X�ւƗA�������B
�E �\�ʂŌő̂���t�̂ւƑ��ω��������́A��Ђ̓����ւ��݂��݁A���q���̉��x��������������B
�܂��A�����̂��Ƃ���A�O�C����̗A�������M�́A�S�Đ�З��q�\�ʂ̗Z���Ɏg����ƍl���Ă悢�B
2) �Z�𒆂̗��q�̔M�̃o�����X
�O�C����̔M�̗A���ƗZ���̐��M�̃o�����X�́A��t���ԂɗZ������\�ʂ̕X�̌�������R�Ƃ���ƁA�����ŕ\�������B���ӁF���q�ɓ����Ă���M�̃t���b�N�X�B�E�ӁF���a�̕ω�
![]()
������Lf�͕X�̗Z���̐��M�A��i�͐�Ђ̖��x�ł���B
�O�q�̂悤��a=b�ł���Ƃ���A�Z���ɔ�����Ђ̔��a�̕ω��͎����̂悤�ɂȂ�B
![]() �@�@�@�@�@�@�@�i�P�j
�@�@�@�@�@�@�@�i�P�j
���ۂɃÂ𑪒肵�������ł͊O�C�͂قڑ��Ύ��x100���ƂȂ��Ă���A�����C���x�̍��͏������Ȃ��Ă����B���������āA�Z���ɔ�����В��a�̕ω��͎����ŕ\�����B
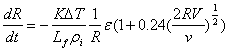
�����łu�͋C���̑��x�A���͋�C�̓��S���W���ł���B
3) �������a��ς��Ď���
14�̐�Ђ�ΏۂɁA�q�̎��ԕω���f�ʐς̕ω��ŕ]�����āA�Â����߂��B�����͈قȂ鏉�����a(4���������10����)�ɂ���Ď��{���ꂽ���A���a�ɂ��Â̕ω��͏����������B�����ł��ׂĂ̐�Ђɂ��ē����l�ƂȂ�ƍl�����A14�̕��ςŃ�=1.75������ꂽ�B(���q���ʉ����Ă���̂ŁA��C�Ƃ̐ږʐς��傫���Ȃ�Â͂P���傫���A�ƍl����)
�����ɗp����ꂽ���l�͈ȉ��̒ʂ�ł���B
![]() (��C�̔M�`����)
(��C�̔M�`����)
![]() (�X�̗Z���̐��M)
(�X�̗Z���̐��M)
![]() (��C�̓��S���W��)
(��C�̓��S���W��)
![]() (��C�Ɛ�Ђ̉��x���A��Ђ�0���Ɖ���)
(��C�Ɛ�Ђ̉��x���A��Ђ�0���Ɖ���)
![]() (�Z�����Ă��Ȃ���Ђ̖��x)
(�Z�����Ă��Ȃ���Ђ̖��x)
![]() (�C���̑��x)
(�C���̑��x)
4) ��W���̈Ӗ�
��W���Â��ς��v���͈ȉ��̓_���l������B
�E ��Ђ̌`�͊��S�ȋ��ł͂Ȃ��B
�E ��Ђ̕\�ʂ̉��ʂɂ���Ēʕ��W�����X��(���炩)�ƈقȂ�\��������B
�E ��Е\�ʂ̋����̉e���B
�܂����̎����œ���ꂽ�Â͈ȉ��̂Ƃ��K�����O�ƂȂ�B
�X����������2�`3�̕X������Ȃ闱�q�̏ꍇ�͗Z�������������q�\�ʂɂƂǂ܂�̂ŁA����̌W���͓��Ă͂܂�Ȃ��B
2-2. ��Ђ̏I�[���x�̎�
(������)��Ђ̒�R�W�����Ђ̒l(Cd=1.2)����J�H�̒l(Cd=0.6)�̒l�܂Ő�Ђ̔��a�q��1�����Ƃ��ċߎ������B
3. �v�Z��
��C���̒�������ʉ߂�������͑�C��Ԃ̕ω����}���Ȃ̂őw��2004�N12��29���̎����ΏۂƂ������B(�v�Z�͍���)
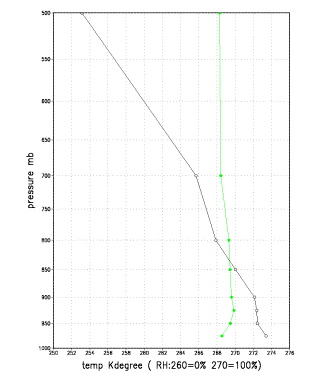
�} 1�@2004�N12��29��9���i�l�r�l�̏����l�j